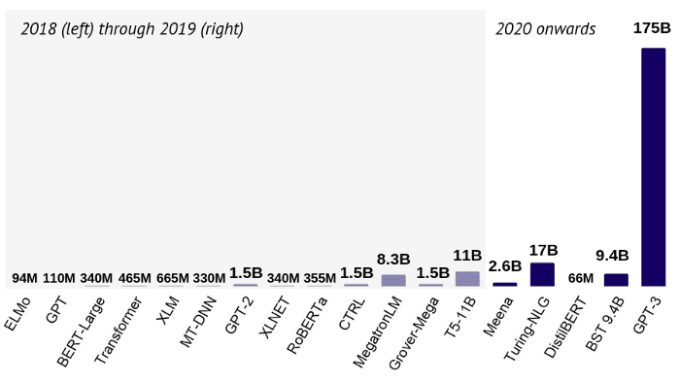
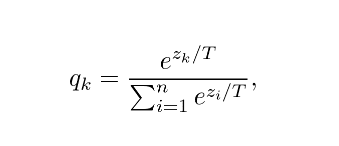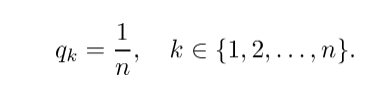To illustrate the point, this is the number of parameters for the most common architectures in (natural language processing) NLP, as summarized in the recent State of AI Report 2020 by Nathan Benaich and Ian Hogarth. You can see this below: In Kaggle competitions, the winner models are often ensembles, composed of several predictors. Although they can beat simple models by a large margin in terms of accuracy, their enormous computational costs make them utterly unusable in practice. [Read: What audience intelligence data tells us about the 2020 US presidential election] Is there any way to somehow leverage these powerful but massive models to train state of the art models, without scaling the hardware? Currently, there are three main methods out there to compress a neural network while preserving the predictive performance:
Weight pruning Quantization Knowledge distillation
In this post, my goal is to introduce you to the fundamentals of knowledge distillation, which is an incredibly exciting idea, building on training a smaller network to approximate the large one.
So, what is knowledge distillation?
Let’s imagine a very complex task, such as image classification for thousands of classes. Often, you can’t just slap on a ResNet50 and expect it to achieve 99% accuracy. So, you build an ensemble of models, balancing out the flaws of each one. Now you have a huge model, which, although performs excellently, there is no way to deploy it into production and get predictions in a reasonable time. However, the model generalizes pretty well to the unseen data, so it is safe to trust its predictions. (I know, this might not be the case, but let’s just roll with the thought experiment for now.) What if we use the predictions from the large and cumbersome model to train a smaller, so-called student model to approximate the big one? This is knowledge distillation in essence, which was introduced in the paper Distilling the Knowledge in a Neural Network by Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. In broad strokes, the process is the following.
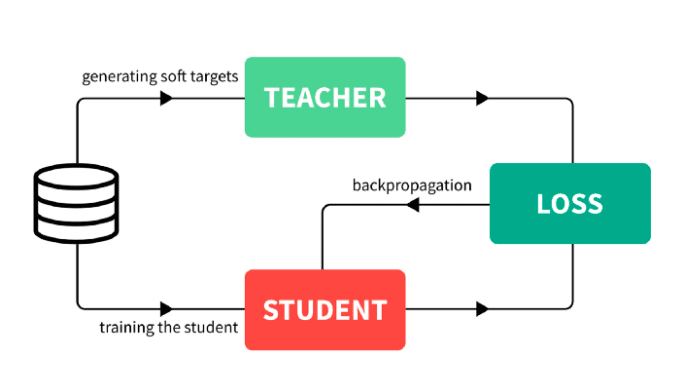
Train a large model that performs and generalizes very well. This is called the teacher model. Take all the data you have, and compute the predictions of the teacher model. The total dataset with these predictions is called the knowledge, and the predictions themselves are often referred to as soft targets. This is the knowledge distillation step. Use the previously obtained knowledge to train the smaller network, called the student model.
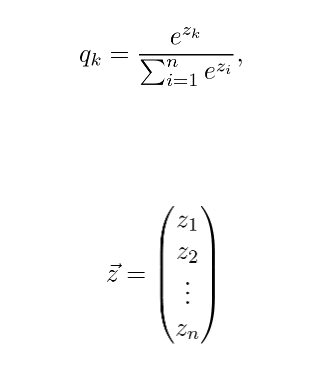
To visualize the process, you can think of the following. Let’s focus on the details a bit. How is the knowledge obtained? In classifier models, the class probabilities are given by a softmax layer, converting the logits to probabilities:
The logits produced by the last layer. Instead of these, a slightly modified version is used:
Where T is a hyperparameter called temperature. These values are called soft targets. If T is large, the class probabilities are “softer”, that is, they will be closer to each other. In the extreme case, when T approaches infinity,
If T = 1, we obtain the softmax function. For our purposes, the temperature is set to higher than 1, thus the name distillation. Hinton, Vinyals, and Dean showed that a distilled model can perform as good as an ensemble composed of 10 large models.
Why not train a small network from the start?
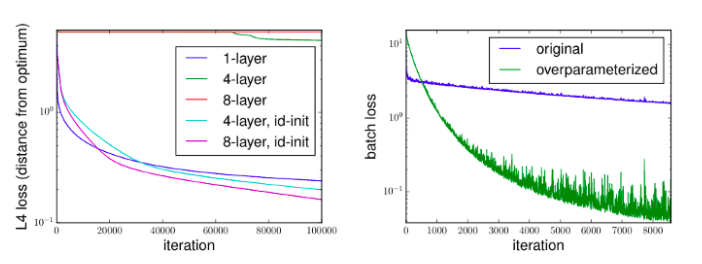
You might ask, why not train a smaller network from the start? Wouldn’t it be easier? Sure, but it wouldn’t work necessarily. Empirical evidence suggests that more parameters result in better generalization and faster convergence. For instance, this was studied by Sanjeev Arora, Nadav Cohen, and Elad Hazan in their paper On the Optimization of Deep Networks: Implicit Acceleration by Overparameterization. For complex problems, simple models have trouble learning to generalize well on the given training data. However, we have much more than the training data: the teacher model’s predictions for all the available data. This benefits us in two ways. First, the teacher model’s knowledge can teach the student model how to generalize via available predictions outside the training dataset. Recall that we use the teacher model’s predictions for all available data to train the student model, instead of the original training dataset. Second, the soft targets provide more useful information than class labels: it indicates if two classes are similar to each other. For instance, if the task is to classify dog breeds, information like “Shiba Inu and Akita are very similar” is extremely valuable regarding model generalization.
The difference between transfer learning
As noted by Hinton et al., one of the earliest attempts to compress models by transferring knowledge was to reuse some layers of a trained ensemble, as done by Cristian Buciluǎ, Rich Caruana, and Alexandru Niculescu-Mizil in their 2006 paper titled Model compression. In the words of Hinton et al., “…we tend to identify the knowledge in a trained model with the learned parameter values and this makes it hard to see how we can change the form of the model but keep the same knowledge. A more abstract view of the knowledge, that frees it from any particular instantiation, is that it is a learned mapping from input vectors to output vectors.” — Distilling the Knowledge in a Neural Network Thus, the knowledge distillation doesn’t use the learned weights directly, as opposed to transfer learning.
Using decision trees
If you want to compress the model even further, you can try using even simpler models like decision trees. Although they are not as expressive as neural networks, their predictions can be explained by looking at the nodes individually. This was done by Nicholas Frosst and Geoffrey Hinton, who studied this in their paper Distilling a Neural Network Into a Soft Decision Tree. They showed that distilling indeed helped a little, although even simpler neural networks have outperformed them. On the MNIST dataset, the distilled decision tree model achieved 96.76% test accuracy, which was an improvement from the baseline 94.34% model. However, a straightforward two-layer deep convolutional network still reached 99.21% accuracy. Thus, there is a trade-off between performance and explainability.
Distilling BERT
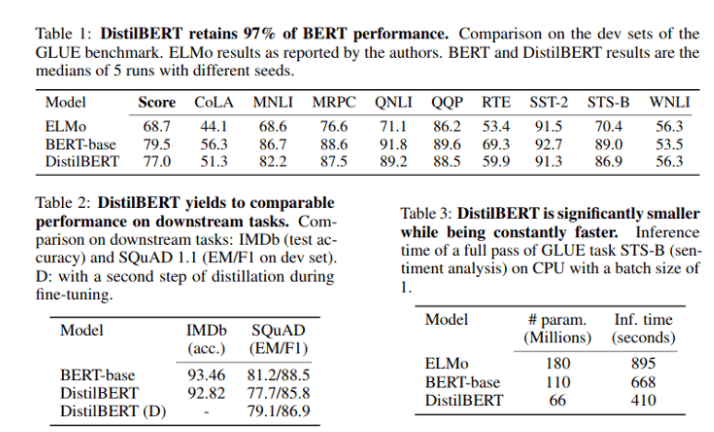
So far, we have only seen theoretical results instead of practical examples. To change this, let’s consider one of the most popular and useful models in recent years: BERT. Originally published in the paper BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding by Jacob Devlin et al. from Google, it soon became widely used for various NLP tasks like document retrieval or sentiment analysis. It was a real breakthrough, pushing state of the art in several fields. There is one issue, however. BERT contains ~110 million parameters and takes a lot of time to train. The authors reported that the training required 4 days using 16 TPU chips in 4 pods. Calculating with the currently available TPU pod pricing per hour, training costs would be around 10000 USD, not mentioning the environmental costs like carbon emissions. One successful attempt to reduce the size and computational cost of BERT was made by Hugging Face. They used knowledge distillation to train DistilBERT, which is 60% the original model’s size while being 60% faster and keeping 97% of its language understanding capabilities. The smaller architecture requires much less time and computational resources: 90 hours on 8 16GB V100 GPUs. If you are interested in more details, you can read the original paper DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter, or the summarizing article was written by one of the authors. This is a fantastic read, so I strongly recommend you to do so.
Conclusion
Knowledge distillation is one of the three main methods to compress neural networks and make them suitable for less powerful hardware. Unlike weight pruning and quantization, the other two powerful compression methods, knowledge distillation does not reduce the network directly. Rather, it uses the original model to train a smaller one called the student model. Since the teacher model can provide its predictions even on unlabelled data, the student model can learn how to generalize like the teacher. Here, we have looked at two key results: the original paper, which introduced the idea, and a follow-up, showing that simple models such as decision trees can be used as student models.